算法设计与分析-Week21

发表于

Linked List Cycle II

题目描述

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Note:
Do not modify the linked list.

Example 1:

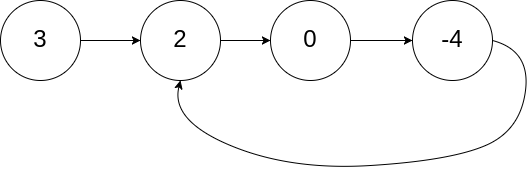
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

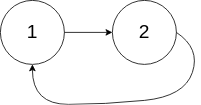
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

解题思路

本题要在一个有环的链表中找环的入口点。
链表寻环最常见的解法就是使用竞速法，用一对快慢指针去遍历链表，如果链表中有环，那么快指针必定会从慢指针后面追上慢指针。本题还要求环的入口点，假设环入口距离链表头的长度为L，环的长度为R，快慢指针相遇的位置为cross，且该位置距离环入口的长度为S。考虑快慢指针移动的距离，慢指针走了L+S，快指针走了L+S+nR(假设相遇之前快指针已经绕环n圈)。由于快指针的速度是慢指针的两倍，那么快指针走的距离也是慢指针的两倍，所以有2(L+S)=L+S+nR，化简得L+S=nR，即L=nR-S=(n-1)R+R-S，此时我们可以用两个指针，一个从链表头开始走，一个从快慢指针相遇点开始走，那么第一个节点走L距离到达环的入口点，第二个节点走（n-1）个环（回到原点）之后，再往前走R-S的距离（即走到环入口点的距离）。所以此时两个节点走了相同的距离并在环的入口点相遇。

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow = head;
        ListNode* fast = head;
        while(fast != NULL && fast->next != NULL) {
            slow = slow->next;
            fast = fast->next->next;
            if(slow == fast) break;
        }
        if(fast == NULL || fast->next == NULL) {
            return NULL;
        }
        ListNode* p1 = head;
        ListNode* p2 = slow;
        while(p1 != p2) {
            p1 = p1->next;
            p2 = p2->next;
        }
        return p1;
    }
};
0%