算法设计与分析-有容量设施选址问题

发表于 | 更新于

Capacitated Facility Location Problem

题目描述

Suppose there are n facilities and m customers. We wish to choose:
(1) which of the n facilities to open
(2) the assignment of customers to facilities
The objective is to minimize the sum of the opening cost and the assignment cost.

Note: The total demand assigned to a facility must not exceed its capacity.

input: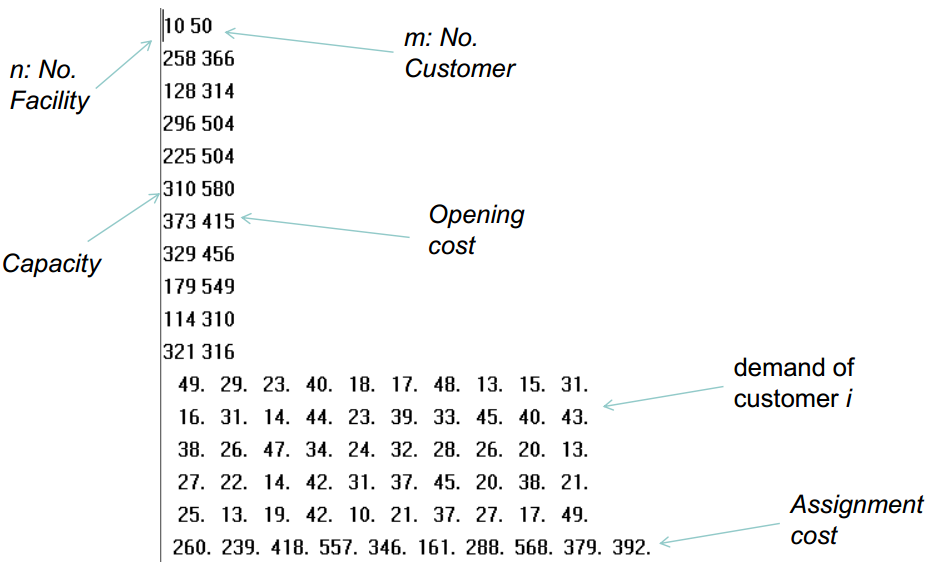
图1

解题思路

算法一：贪心算法

该算法主要的贪心策略为：创建一个bool二维数组alloc，alloc[i][j]表示第i个顾客可以分配到第j个设施。在整个assignmentCost表中找到cost最小且可以被分配的assignmentCost[i][j]，该cost对应顾客i和设施j，如果该设施没有足够的容量给该顾客，那么将alloc[i][j]标记为false；如果该设施有足够的容量，就将该顾客分配给该设施，并将alloc[i]标记为false。

主要代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
/*
获取贪心算法执行后的状态
State.cost:该状态的费用
State.occupy:每个设施已分配的空间
State.assign:每个顾客所分配的设施
*/
State Greedy::getBestState() {
	vector<int> assign(customer, -1);
	vector<double> occupy(facility, 0);
	vector<vector<bool>> alloc(customer, vector<bool>(facility, true));
	for (int i = 0; i < customer; i++) {
		int custom, faci;
		while (true) {
			findMin(alloc, custom, faci);
			/*该设施容量足够*/
			if (occupy[faci] + demand[custom] <= capacity[faci]) {
				for (int j = 0; j < alloc[custom].size(); j++) {
					alloc[custom][j] = false;
				}
				occupy[faci] += demand[custom];
				assign[custom] = faci;
				break;
			}
			/*该设施容量不够*/
			else {
				alloc[custom][faci] = false;
			}
		}
	}
	double cost = calculateCost(occupy, assign); //计算cost
	return State(cost, occupy, assign);
}

/*
找到cost最小且可以被分配的顾客和设施
alloc[i][j]:顾客i是否可以分配到设施j
custom:找到的顾客
faci:找到的设施
*/
void Greedy::findMin(const vector<vector<bool>> &alloc, int &custom, int &faci) {
	int m = INT_MAX;
	for (int i = 0; i < assignmentCost.size(); i++) {
		for (int j = 0; j < assignmentCost[i].size(); j++) {
			if (alloc[i][j] && assignmentCost[i][j] < m) {
				m = assignmentCost[i][j];
				custom = i;
				faci = j;
			}
		}
	}
}

/*
计算cost
occupy:每个设施已分配的空间
assign:每个顾客分配的设施
*/
double Greedy::calculateCost(const vector<double> &occupy, const vector<int> &assign) {
	double cost = 0;
	for (int i = 0; i < facility; i++) {
		cost += (occupy[i] > 0) ? openCost[i] : 0; //判断该设施是否已分配，如果是，则加上开启该设施的代价
	}
	for (int i = 0; i < customer; i++) {
		cost += assignmentCost[i][assign[i]];
	}
	return cost;
}

输出

ResultTime(s)
p193070.005
p279930.004
p399930.005
p4119930.004
p592200.005
p679060.004
p799060.005
p8119060.004
p990400.005
p1077260.004
p1197260.006
p12117260.004
p13120320.007
p1491800.007
p15131800.008
p16171800.009
p17120320.009
p1891800.009
p19131800.008
p20171800.009
p21120320.009
p2291800.008
p23131800.008
p24171800.008
p25192480.054
p26161820.054
p27215820.055
p28269820.054
p29192240.054
p30161580.072
p31215580.053
p32269580.056
p33190550.054
p34159890.054
p35213890.055
p36267890.056
p37190550.052
p38159890.053
p39213890.054
p40267890.055
p4171030.009
p4299570.015
p43124480.018
p4472220.009
p4598480.016
p46126390.018
p4764900.009
p4890440.015
p49124200.018
p50100600.011
p51113960.019
p52107640.012
p53128340.022
p54101430.011
p55119380.022
p56238820.087
p57328820.083
p58538820.081
p59391210.084
p60238820.081
p61328820.082
p62538820.082
p63391210.083
p64238820.082
p65328820.082
p66538820.084
p67396710.085
p68238820.082
p69328820.08
p70538820.081
p71391210.082

算法二：模拟退火

模拟退火算法是一种通用概率演算法，用来在一个大的搜寻空间内找寻命题的最优解。其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法是一种通用的优化算法，其物理退火过程由加温过程、等温过程、冷却过程这三部分组成。
模拟退火最重要的部分就是状态产生函数，我在实现中随机采用三种邻域搜索策略的其中一种，一是随机将一位顾客转移到另一个设施，二是随机交换两位顾客，三是随机关闭一个设施。除此之外，模拟退火通常还有一些参数需要手动调整，如初温，末温，降温系数，内循环迭代次数等。

主要代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
/*
模拟退火过程
beginTem:初温
endTem:末温
cool:降温系数
iteration:内循环迭代次数
*/
void SA::run(double beginTem, double endTem, double cool, int iteration) {
	/*十次模拟退火过程取其中最好的一次*/
	for (int count = 0; count < 10; count++) {
		genRandomState(); //随机产生一个当前状态
		bestStateForEveryIteration = curState; //记录每次循环的最好状态
		double tem = beginTem;
		/*模拟退火主过程*/
		while (tem >= endTem) {
			for (int i = 0; i < iteration; i++) {
				int ran = rand() % 5; //产生一个随机数，根据随机数选择邻域策略
				/*随机关闭一个设施*/
				if (ran < 1) {
					State nextState = closeRandomFacility();
					if (exp((curState.cost - nextState.cost) / tem) >= rand() % 100 / 100.0) {
						curState = nextState;
					}
				}
				/*随机交换两位顾客*/
				else if (ran < 3) {
					State nextState = exchangeTwoCustomer();
					if (exp((curState.cost - nextState.cost) / tem) >= rand() % 100 / 100.0) {
						curState = nextState;
					}
				}
				/*随机将一位顾客转移到另一个设施*/
				else {
					State nextState = moveCustomerToAnotherFacility();
					if (exp((curState.cost - nextState.cost) / tem) >= rand() % 100 / 100.0) {
						curState = nextState;
					}
				}
				/*更新本次循环的最好状态*/
				if (curState.cost < bestStateForEveryIteration.cost) {
					bestStateForEveryIteration = curState;
				}
			}
			tem *= cool; //降温
		}
		cout << bestStateForEveryIteration.cost << endl;
		/*保存十次循环的最好状态*/
		if (bestStateForEveryIteration.cost < bestState.cost)
			bestState = bestStateForEveryIteration;
	}
}

/*随机产生一个初始状态*/
void SA::genRandomState() {
	while (true) {
		curState.assign = vector<int>(customer);
		curState.occupy = vector<double>(facility, 0);
		for (int i = 0; i < customer; i++) {
			curState.assign[i] = rand() % facility;
			curState.occupy[curState.assign[i]] += demand[i];
		}
		if (isFeasible(curState.occupy)) {
			curState.cost = calculateCost(curState.occupy, curState.assign);
			break;
		}
	}
}

/*随机将一位顾客转移到另一个设施*/
State SA::moveCustomerToAnotherFacility() {
	while (true) {
		int index = rand() % customer; //随机选择一位顾客
		int newFacility = rand() % facility; //随机选择一个设施
		if (curState.occupy[newFacility] + demand[index] <= capacity[newFacility]) {
			State nextState = curState;
			nextState.occupy[nextState.assign[index]] -= demand[index];
			nextState.assign[index] = newFacility;
			nextState.occupy[newFacility] += demand[index];
			nextState.cost = calculateCost(nextState.occupy, nextState.assign);
			return nextState;
		}
	}
}

/*随机交换两位顾客*/
State SA::exchangeTwoCustomer() {
	while (true) {
		int index1 = rand() % customer; //随机选择顾客1
		int index2 = rand() % customer; //随机选择顾客2
		if (curState.occupy[curState.assign[index1]] - demand[index1] + demand[index2] <= capacity[curState.assign[index1]]
			&& curState.occupy[curState.assign[index2]] - demand[index2] + demand[index1] <= capacity[curState.assign[index2]]) {
			State nextState = curState;
			nextState.occupy[nextState.assign[index1]] = nextState.occupy[nextState.assign[index1]] - demand[index1] + demand[index2];
			nextState.occupy[nextState.assign[index2]] = nextState.occupy[nextState.assign[index2]] - demand[index2] + demand[index1];
			int temp = nextState.assign[index1];
			nextState.assign[index1] = nextState.assign[index2];
			nextState.assign[index2] = temp;
			nextState.cost = calculateCost(nextState.occupy, nextState.assign);
			return nextState;
		}
	}
}

/*随机关闭一个设施*/
State SA::closeRandomFacility() {
	int closeFacility = rand() % facility; //随机选择一个要关闭的设施
	State nextState = curState;
	nextState.occupy[closeFacility] = 0;
	for (int j = 0; j < customer; j++) {
		/*找到分配到要关闭设施的顾客*/
		if (nextState.assign[j] == closeFacility) {
			while (true) {
				int newFacility = rand() % facility; //随机为该顾客选择一个新设施
				if (nextState.occupy[newFacility] + demand[j] <= capacity[newFacility]) {
					nextState.assign[j] = newFacility;
					nextState.occupy[newFacility] += demand[j];
					break;
				}
			}
		}
	}
	nextState.cost = calculateCost(nextState.occupy, nextState.assign);
	return nextState;
}

/*
判断当前设施的占用状态是否可行
occupy:设施的占用状态
*/
bool SA::isFeasible(const vector<double> &occupy) {
	for (int i = 0; i < occupy.size(); i++) {
		if (occupy[i] > capacity[i]) return false;
	}
	return true;
}

输出

ResultTime(s)
p189502.581
p280112.588
p395252.592
p4110632.643
p591192.786
p678412.702
p797592.721
p8111892.731
p987112.505
p1077672.503
p1191812.509
p12104532.514
p1394442.53
p1480152.523
p1597442.506
p16116792.518
p1792582.495
p1879002.51
p19100072.521
p20119652.53
p2186862.47
p2279092.497
p2398722.464
p24114442.469
p25152144.129
p26140734.123
p27161394.106
p28181264.1
p29154334.127
p30134854.143
p31163444.133
p32193874.145
p33145114.096
p34126364.099
p35154394.108
p36177484.105
p37137324.094
p38135084.093
p39153104.07
p40170694.077
p4169203.215
p4265702.972
p4362712.836
p4479623.294
p4575682.972
p4671712.861
p4770813.298
p4867622.997
p4966642.883
p5092353.424
p5185743.286
p5297353.542
p53101403.29
p5494753.646
p5588093.282
p56292074.951
p57366794.978
p58481924.994
p59386464.996
p60294404.896
p61335824.887
p62434974.898
p63355684.885
p64292474.888
p65331684.875
p66427064.87
p67346104.928
p68283244.896
p69349924.886
p70437084.934
p71350964.938

算法对比

  • 速度：从时间上可以看出，贪心算法运行速度很快，而模拟退火因为每一轮都跑了十次，所以速度较慢。
  • 结果：贪心算法的结果没有模拟退火好。尤其是贪心策略没有考虑设施开启时的费用，仅考虑分配顾客时的费用，容易陷入局部最优。而模拟退火在整个大的搜索空间求解，并通过几种邻域搜索策略，即使陷入局部最优解，也有几率可以跳出，最终得到的解与全局最优解更加接近。

实验思考

在实现贪心算法时，我后来考虑到了把设施的开启费用加进去，我将整个顾客分配损失表assignmentCost每一列加上了对应设施的开启费用，然后重复之前的贪心策略，选取费用最小的进行分配，如果分配成功且之前该设施未开启，就把assignmentCost的该列减去开启费用，即开启该设施。然而做了这个改进之后并没有之前的效果好，感觉应该是因为这种贪心策略会使得很多顾客挤在某几个设施。
在实现模拟退火时，一开始我实现了两种邻域搜索策略，即随机将一位顾客分配到另一个设施和随机交换两位顾客，在观察结果时我发现，几乎每个设施都打开了，因此我引入了第三种邻域搜索策略，即随机关闭一个设施，并使得这种操作的概率较低，这样做似乎比较容易跳出局部最优，效果挺好。

具体每个测试样例的详细结果和项目源码请参考：github

0%