Container With Most Water
题目描述
Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
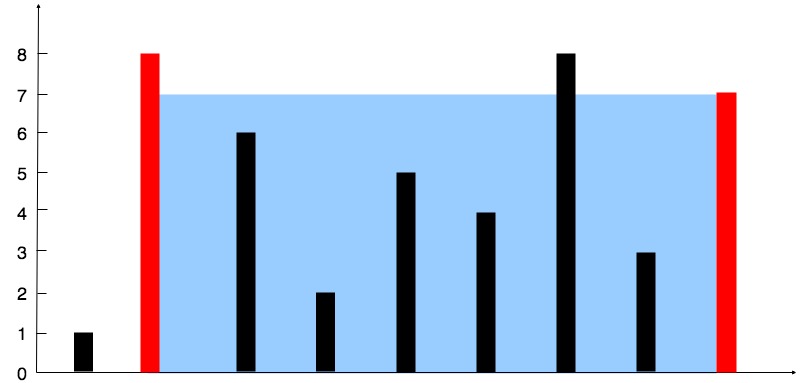
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example:
Input: [1,8,6,2,5,4,8,3,7]
Output: 49
解题思路
题目要求最大可装水的体积,可装水的体积取决于水桶两边的高以及底边的宽度,根据短板效应,可装水的高度不会超过两边的较短边的高度,因此可装水的体积=水桶两边的较短边的高度*底边的宽度。
解法一
暴力求解。将所有边两两组合并求体积,用两重循环即可解决,但时间复杂度为\(O(n^2)\)
解法二
先选取最左边和最右边两条边,记录此时的可装水的体积,由于该体积取决于两边的较短边,因此我们希望该较短边越长越好,于是我们将较短边替换成更内层的边,并计算新的可装水体积,与原来的体积作比较取较大值。最后当两边取到同一边时退出循环,得到最大可装水体积,时间复杂度为\(O(n)\)
源代码
1 | class Solution { |